MATEMATICAS GRADO 9, SEMANAS 5 Y 6, PERIODO 1, AÑO 2021

 CRITERIOS DE CONGRUENCIA Y SEMEJANZA DE TRIÁNGULOS

CONGRUENCIA

Dos objetos geométricos son congruentes si tienen las mismas medidas y los mismos ángulos.

Ejemplos:

En segmentos  
     
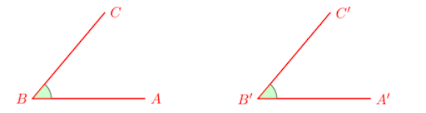
En ángulos        

son congruentes porque tienen la misma medida.

son congruentes porque tienen la misma medida.

Existen tres criterios para determinar si dos triángulos dados son o no congruentes.

Los criterios son los siguientes:

1 Si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, los dos triángulos son congruentes.

2 Si un ángulo de un triángulo es congruente con el ángulo de otro triángulo, y además los lados del ángulo considerado en cada triángulo son congruentes, entonces los dos triángulos son congruentes.

3 Si las longitudes de los lados de un triángulo son congruentes a las longitudes de los lados de otro triángulo, entonces los dos triángulos son congruentes.

Teoremas sobre la congruencia de triángulos:

A. Todo triángulo es congruente a sí mismo.

se escribe:  

B. Si un triángulo es congruente a otro triángulo, el segundo es congruente al primero.

se escribe:

C. Si un primer triángulo es congruente a un segundo triángulo, y a su vez este segundo triángulo es congruente a otro tercer triángulo, entonces el primero y el tercero son congruentes. Es decir, la congruencia entre triángulos tiene la propiedad transitiva.

se escribe:

Actividad 1.

Dibujar cuatro objetos (diferentes a los ejemplos dados ) que sean congruentes y explica porqué lo son. 

LEER NOTA ABAJO

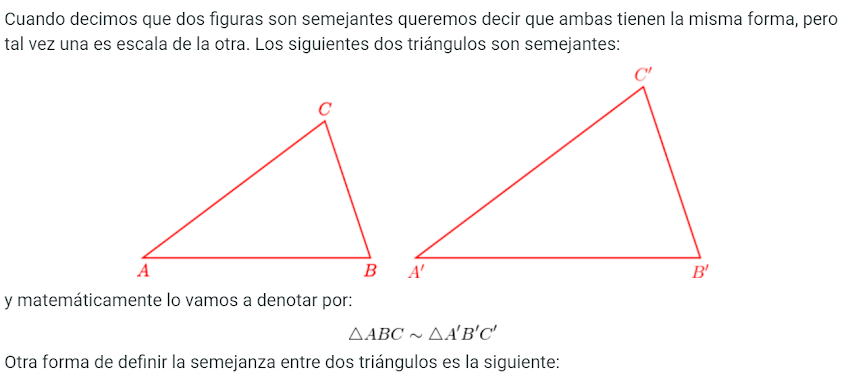
SEMEJANZA

Dos figuras geométricas son semejantes si tienen los mismos ángulos internos (uno a uno) y sus lados correspondientes tienen la misma proporción.

Ejemplos:

A. 

B. 

Actividad 2.

Dibujar cuatro objetos (diferentes a los ejemplos dados)que sean semejantes y explica porqué lo son.

Hay que ser creativos!!!!

LEER NOTA ABAJO.

NOTA

Están  enviando las mismas figuras y ejemplos.

Se pide dibujar objetos diferentes, que no sean ni triángulos, ni cuadrados, pueden ser casas, cubos, fachadas de edificios, mesas,  sillas, etc, etc, etc.